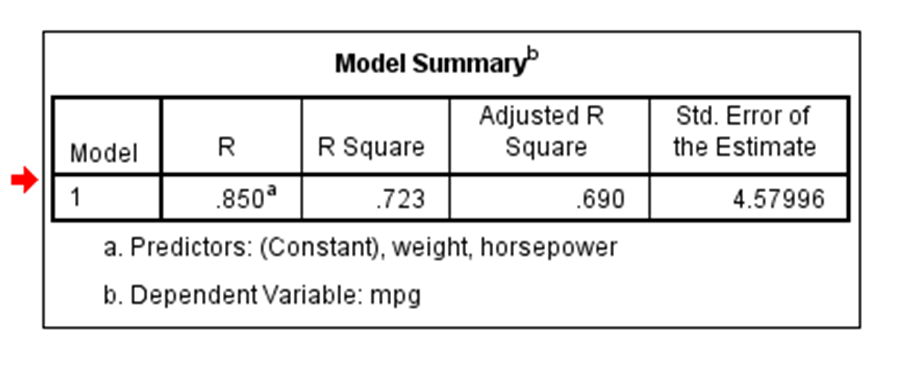
Coefficient of correlation is “R” value which is given in the summary table in the Regression output. R square is also called coefficient of determination. Multiply R times R to get the R square value. In other words Coefficient of Determination is the square of Coefficeint of Correlation.
R square or coeff. of determination shows percentage variation in y which is explained by all the x variables together. Higher the better. It is always between 0 and 1. It can never be negative – since it is a squared value.
It is easy to explain the R square in terms of regression. It is not so easy to explain the R in terms of regression.
Coefficient of Correlation: is the degree of relationship between two variables say x and y. It can go between -1 and 1. 1 indicates that the two variables are moving in unison. They rise and fall together and have perfect correlation. -1 means that the two variables are in perfect opposites. One goes up and other goes down, in perfect negative way. Any two variables in this universe can be argued to have a correlation value. If they are not correlated then the correlation value can still be computed which would be 0. The correlation value always lies between -1 and 1 (going thru 0 – which means no correlation at all – perfectly not related). Correlation can be rightfully explalined for simple linear regression – because you only have one x and one y variable. For multiple linear regression R is computed, but then it is difficult to explain because we have multiple variables invovled here. Thats why R square is a better term. You can explain R square for both simple linear regressions and also for multiple linear regressions.

Dear Gaurav,
I would differ from what you are referring to as Coefficient of Determination.
Actually, herein the Coefficient of Determination has been defined as the square of the coefficient of correlation, which is not correct, as per my understanding. It is also mentioned that R square can never be negative since it is a square, whereas in much statistical analysis, the actual coefficient of Determination is obtained as negative, that refers to fit even worse than the average values.
So, as per my understanding, One term is the Coefficient of Determination, and the other term is Square of the coefficient of correlation (r).
Looking forward to your reply on this.
Thank you for your explanation it really helped me
nice. very helpful. precise and clear explanation.