A heat engine is a system that uses energy in form of heat and transforms it in mechanical work and then exhausts the heat which cannot be used to do work. It does it by bringing a working substance from a higher state temperature to a lower state temperature.

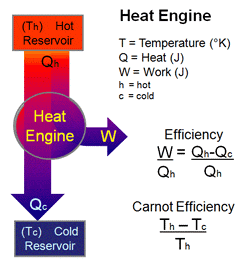
A hot source generates the thermal energy that brings the working substance to the high temperature state. The working substance generates work in the working body of the engine while transferring heat to the colder sink until it reaches a low temperature state. During this process some of the thermal energy is converted into work by exploiting the properties of the working substance.