Refrigerators are devices that that will transfer heat from a low temperature environment to a high temperature environment. Thermodynamics refrigeration cycles are the conceptual and mathematical models for refrigerators. Refrigerators and heat pumps are essentially the same device; they only differ in their objectives.
There are different refrigeration cycles, but all of them has four main components:
- Evaporator
- Compressor
- Condenser
- Turbine/Expansion valve
Although all cycle has the same elements, there are different refrigeration cycles. The most important refrigeration cycles are:
- Reversed Carnot Cycle
- Ideal Vapor-Compression Refrigeration Cycle
- Actual Vapor-Compression Refrigeration Cycle
Reversed Carnot Cycle
Reversing the Carnot cycle does reverse the directions of heat and work interactions. A refrigerator or heat pump that operates on the reversed Carnot cycle is called a Carnot Refrigerator.
It has the maximum efficiency for a given temperature limit. Also, since it is a reversible cycle, all four processes can be reversed.
| Process | Description |
| 1-2 | Isothermal heat transfer from cold medium to refrigerant |
| 2-3 | Isentropic compression |
| 3-4 | Isothermal heat rejection |
| 4-1 | Isentropic Expansion |
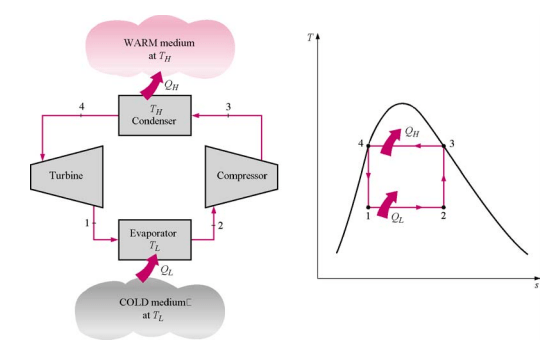
Ideal Vapor-Compression Refrigeration Cycle
The most widely used refrigeration cycle is the vapor-compression refrigeration cycle, the refrigerant enters the compressor as saturated vapor and is cooled to the saturated liquid state in the condenser. It is then throttled too the evaporator pressure and vaporizes as it absorbs heat from the refrigerated space.
The impracticalities of the reversed Carnot Cycle can be eliminated by:
- Vaporising the refrigerant completely before it is compressed
- Replacing the turbine by a throttle valve
- By implication; isothermal processes are replaced by constant pressure processes.
Also, we have to make some assumptions for ideal vapor-compression cycle:
- Irreversibilities within the evaporator, condenser and compressor are ignored
- No frictional pressure drops
- Refrigerant flows at constant pressure through the two heat exchangers (evaporatorand condenser)
- Heat losses to the surroundings are ignored
- Compression process is isentropic
The ideal vapor-compression cycle consists of four processes:
| Process | Description |
| 1-2 | Isentropic Compression |
| 2-3 | Constant Pressure Heat rejection in the condenser |
| 3-4 | Throttling in an expansion valve |
| 4-1 | Constant pressure heat addition in the evaporator |
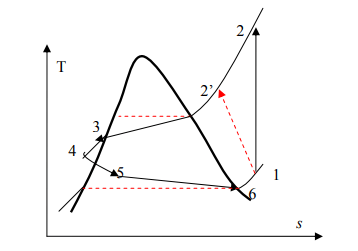
Actual Vapor-Compression Refrigeration Cycle
It is the real application of the ideal vapor-compression refrigeration cycle. The two main differences between both of them are the fluid frictions, that causes pressure drop and the heat transfer to or from surroundings.
| Process | Description |
| 1-2 | Irreversible and non-adiabatic compression of refrigerant. Heat transfer from surroundings to refrigerant and entropy increases |
| 1-2’ | Heat transfer from refrigerant to surroundings and S2′<S1 |
| 2-3 | Temperature (and pressure) drop due to fluid friction and heat transfer |
| 3-4 | Pressure drops in the condenser because of fluid friction |
| 4-5 | Temperature and pressure drop (As in 2-3) |
| 5-6 | Throttling process |
| 6-7 | The throttle valve and evaporator are usually located very close to each other, so pressure drop in connecting line is small. |
Best efficiency based on Thermodynamics
The efficiency of a refrigerator or heat pump is given by a parameter called the coefficient of performance (COP).
As we can see, in this scenario QL is the desired output, which for a refrigerator is the cooling effect (the amount of heat removed). So the efficiency is the amout of heat removed per amount of work input.
Expressed in terms of Temperature:
COP = TL/(TH-TL)
Being TL low-temperature and TH, high-temperature.
This equation is limited by Carnot’s theorem, so in a real cycle, COP needs to be equal or less that that.
This means that the best efficiency based on Thermodynamics (which is what we are trying to find) is defined by the following formula:
For Carnot refrigerators::
COPR,Carnot = 1/((TH/TL) – 1)
We use the “coefficient of performance instead of just “efficiency” because the first one measures the amount of heat that we are moving. We are indeed moving heat, not creating it, that is why some coefficients of performance can be greater than one (e.g.: in a heat pump we can move more heat than the input work. Therefore, the equation that relates these two coefficients (the heat pump one and the refrigerator one) is the following:
COPheating – COPcooling = 1
Where COPheating is the coefficient of performance of the heat pump, which is the same as COPr (refrigerator) but taking in consideration that here, the desired effect (See first equation of this part) is the heating effect, not cooling.
Just as a fact, there is a term called ‘thermal efficiency’ (sometimes called energy efficiency). In the United States, there is a common way of measuring the efficiency of cooling devices, which is ruled by the SEER (Seasonal Energy Efficiency Ratio), defined by Air Conditioning, Heating, and Refrigeration Institute in 2008 . This is useful when it comes to calculations about electricity and energy waste, and calculations of costs based on the efficiency of the devices.
We talked above about the best efficiency based on Thermodynamics, but it is also interesting to see how we can improve the coefficient of performance in order to aim for the highest efficiency possible.
In a cooling device, like the refrigerator, the COP can be improved by using ground water as an input instead of air, and by reducing temperature drop on output side through increasing air flow.
If we look strictly to the equation, increasing TL would increase the COP.
But, taking in consideration some other parameters, some useful ways of increasing the efficiency are increasing the size of pipes and air canals, which would help to reduce noise and energy consumption.
Also, reducing the gap between TL and TH should work too in order to achieve a higher efficiency.
Engineering Details of a Refrigerator
Front of Refrigerator:
Back of Refrigerator:
Interior of Refrigerator:
Throttling Device: device used to produce cold liquid
The throttling device is composed of a capillary tube which has a diameter of roughly 0.6 mm and a length of 2 m. High pressured liquid enters the throttling device. The throttling device will act as an obstruction to the flow of the high-pressured liquid and will result in a pressure drop. The pressure dropping will cause the boiling point of the refrigerant to come down and the refrigerant starts to evaporate.
Heat required for evaporation comes within the refrigerant so its temperature drops.
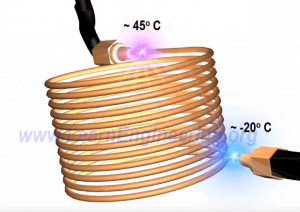
This drop results in a temperature drop at the top of the capillary tube vs the bottom of the capillary tube.
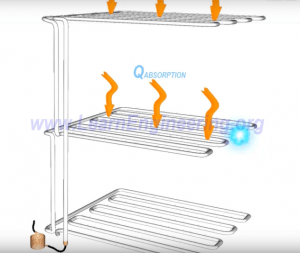
Pass cold liquid over throughout the refrigerator.
Heat is then absorbed.
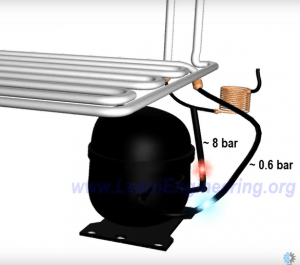
During heat absorption process, the refrigerant further evaporates and transforms into pure vapor. Thus to begin the entire process again, the low pressure vapor refrigerant will have to be converted back to high pressured liquid. Thereby, a compressor is introduced to raise the pressure back to its initial value.
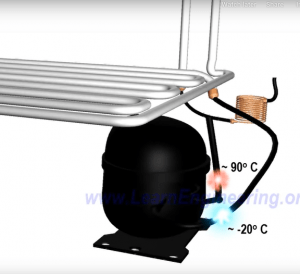
The compressor increases the refrigerants pressure, and thus also increases the temperature of the refrigerant.
Now the refrigerant is composed of high-pressure vapor. To convert the refrigerant to liquid, another heat exchanger is needed. This heat exchanger is fitted outside the refrigerator to allow the heat to be released to the surroundings.
Vapor will get condensed to liquid and temperature will come down to a normal level. Thereby the refrigerant is back to its original state, which is high pressure liquid.
This cycle can be repeated for continuous refrigeration
Energy of Refrigerator System
Environmental Impacts of Refrigeration:
- Cooling Appliances like Refrigerators
- Contain many hazardous and toxic materials
- Pre-1995 cooling appliances contain:
- chlorofluorocarbons (CFCs) or hydrochlorofluorocarbons (HCFCs)
- ozone-depleting substances (ODSs)
- Potent greenhouse gases (GHGs).
- Pre-2000 freezers (some):
- contain 1 to 1.5 grams of mercury
- highly toxic
- New cooling appliances contain:
- hydrofluorocarbons (HFCs)
- no impact on the ozone layer
- potent GHGs
- The United States, Canada and Mexico are lobbying to reduce HFC use
- contain halocarbons
- Where:
- refrigeration system
- foam insulation
- Impact:
- When these gases are not trapped and destroyed, they have a major impact on atmospheric warming
- (700 to 10,900 times that of CO₂)
- Thus a Recycling problem exists
- A refrigerator thrown in the garbage, releases up to 3.7 metric tons of CO₂ equivalent, which is the same amount emitted by a car that travels 17,500 km
- When these gases are not trapped and destroyed, they have a major impact on atmospheric warming
- Where:
- hydrofluorocarbons (HFCs)
- contain 1 to 1.5 grams of mercury
- Pre-1995 cooling appliances contain:
- Contain many hazardous and toxic materials
- Result of cooling appliances containing hazardous and toxic materials when thrown out
- Depletion of the ozone layer
- Leads to Climate Change
- Acceleration of climate change
- Massive amounts of CO2 released
- Mercury contamination of the environment
- Contribution to the greenhouse effect
- Why
- Halocarbons
- Prevent heat escaping from the earth and deplete the ozone layer that filters the sun’s rays.
- The greenhouse effect and ozone layer depletion contribute to global warming.
- Prevent heat escaping from the earth and deplete the ozone layer that filters the sun’s rays.
- Halocarbons
- Why
- Depletion of the ozone layer
- Impacts of Climate Change
- Increased health risks
- Extreme weather
- (Floods, droughts, forest fires, etc.)
- Higher sea levels
- Reduced agricultural output
- Reduction in phytoplankton, which feeds many fish
- Changes in wildlife habitats
Properties of the Main Gases Used in Refrigeration and Air Conditioning
| Gas | Use | Global Warming Potential (Metric tons of CO₂ equivalent) | Ozone-Depletion Potential |
| CFC-11 | Foam insulation and industrial coolers | 4750 | 1 |
| CFC-12 | Refrigeration gas | 10 900 | 1 |
| HCFC-141b | Foam insulation | 725 | 0.11 |
| HCFC-22 | Refrigeration gas | 1700 | 0,055 |
| HFC-134a | Refrigeration gas | 1430 | 0 |
Group view point:
Refrigerators are an important part of the 21st Century’s everyday life. Today, we humans take it for granted to be able to conveniently store perishable food for long periods of inside our own homes. However, this has not come without a cost. Refrigerators have multiple types of chemicals that when degraded cause extensive damage to earth’s environment. The future of multiple refrigerators inside homes is unlikely. Instead more efficient and smaller refrigerators will need to be used in order to protect the environment from dangerous chemicals as well as they will need to require less energy to function.
This will need many people to get involved, chemists to research less hazardous refrigerants and engineers trying to optimize its components, aiming for the highest efficiency possible, and putting effort on reducing costs, electricity usage and energy waste.








Recent Comments