Thermodynamic Principle of a Heat Pump
A heat pump is a machine that transfers heat from one place to another. It acts as an air conditioner or a furnace. The process of this machine involves moving air from outdoors to indoors without using a lot of energy. It is able to produce hot and cold air depending on what temperature is desired. On hot days, the heat pump pulls in cold air from outside and is able to cool air inside homes or cars. When it is cold out, it is able to do the same thing but pulls in heat from the air outside to warm environments (4). A heat pump is able to do this using work in the system (figure 1a), because work is added to the system and no energy is created. This type of system is a representation of the Carnot Cycle (figure 1b). There are multiple types of heat pumps; the ones we will discuss are air-to-air, geothermal and water source heat pumps.
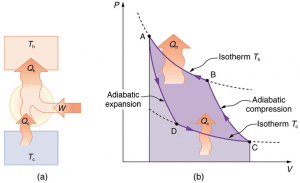
Figure 1a and 1b
Best Efficiency Based on Thermodynamics
When a heat pump is used in conjugation with a gas-furnace, both pieces of equipment share the heating load. They operate at different times, making the efficiency greater. When the temperatures are too low for the heat pump to operate, the gas furnace takes over. When the temperature rises again, the heat pump takes over. This is a cost-efficient dual process because it allows the heat pump to not use any more energy than it has to (3).
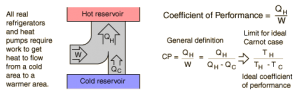
Heat pumps are rated using COP, which stands for Coefficient of Performance (2). A good COP for heating is above 1.2, and for cooling is above 0.7. Heat pumps don’t work well in climates where temperatures fall below freezing often, so you probably wouldn’t be able to find many around Wisconsin. This is because moving heat from a very cold area takes a lot more energy (4). In this case, gas furnaces would be the best option for transferring heat.
Figure 2
Details of the Heat Pump
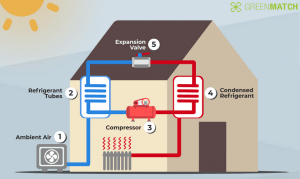
The components of a heat pump include a condenser, expansion valve, evaporator and a compressor (2). When the pump wants to produce warm air, it transfers heat that occurs from the working fluid in the evaporator and uses the cold air outside to turn it into a gas. The compressor is able to increase the temperature and pressure of the gas pushing it into the condenser coils into the heated space. The heat from the gas is transferred into the room as the gas condenses back into a liquid. The working fluid is then cooled as it goes back through the expansion valve then to the outdoor evaporator coils (4). These components are the same for all types of heat pumps.
Figure 3
There are three major types of heat pumps: air to air, water source and geothermal source. Air to air heat pumps use a reverse cycle to move hot and cold air. This pump delivers one and a half to three times more heat than a furnace and uses less energy to do so. Another type of heat pump is geothermal, which absorbs heat from the ground.
A water source heat pump absorbs heat in a similar way, except through underground pipes containing water. These pipes can be closed loop or open loop. In a closed loop pipe, the same water circulates through pipes repeatedly. In an open loop pipe, water is pumped out of the water source, such as a well or lake, heat is extracted, and water returns to the original water source (4). These heat pumps have high efficiency. They typically cost a lot to install, but a lot of money is saved over the years to run it. They fit in most homes and are sturdy to take on extreme weather, unlike air to air heat pumps (1).
Figure 4
Environmental Impacts
Heat pumps are an environmentally friendly alternative to furnaces and air conditioners. They can reduce one’s electricity bill by half. High efficiency pumps also dehumidify better and cool homes faster than air conditioners because they use less energy and are more effective.
Personal Views
Heat pumps are very viable sources that are energy efficient. They are capable of heating many things such as swimming pools, buildings, and hot tubs. What makes heat pumps unique is that they distribute heat evenly throughout an environment. If you’re from Wisconsin, an air to air pump might not be the best idea to invest in because a lot of the time the temperatures here are too cold for heat pumps to work well in the frozen tundra. Air to air pumps are our favorite in the summer because they help keep us cool in the summer while we sit on the couch drinking a mojito.
References
- Heat Pump Systems, Office of Energy Efficiency & Renewable Energy https://www.energy.gov/energysaver/heat-and-cool/heat-pump-systems
- Heat Pump, Wikipedia. https://en.wikipedia.org/wiki/Heat_pump
- What is a Heat Pump? Lennox https://www.lennox.com/help/faqs/heat-pumps
- Cowan, Laura, Sennebogen, Emilie, How Heat Pumps Work. How stuff works https://home.howstuffworks.com/home-improvement/heating-and-cooling/heat-pump.htm
- Figure 1: https://opentextbc.ca/physicstestbook2/wp-content/uploads/sites/211/2017/10/Figure_16_05_01.jpg
- Figure 2: http://hydrogen.physik.uni-wuppertal.de/hyperphysics/hyperphysics/hbase/thermo/imgheat/hpump.gif
- Figure 3:https://www.greenmatch.co.uk/media/2465211/how-air-source-heat-pump-works.png
- Figure 4:https://www.real-world-physics-problems.com/images/geothermal_heat_pump.png

Recent Comments