Fuel cells are widely used in many different applications requiring the use of electricity, which range anywhere from buildings to electronic devices such as phones and laptop computers.
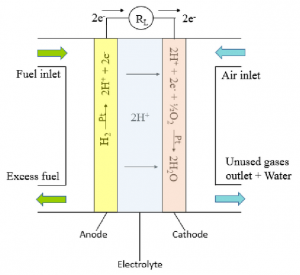
Fuel cells work similarly to how batteries do, except that they do not run down or need recharging; fuel cells only require a fuel source that is fed to the anode (such as hydrogen in a hydrogen fuel cell) and air that is fed to the cathode in order to produce electricity. A catalyst (in the diagram above, it’s platinum) is also present in hydrogen fuel cells to assist in the process of separating protons from electrons, which then take their separate paths. The electrons flow through an external circuit, thus generating electricity there. The protons flow through the electrolyte straight to the cathode and combine with oxygen and the electrons there to produce water and heat.
Fuel cell engineers are continuously trying to find new ways to make these more efficient while also making them more environmentally friendly. These can be engineered simply for classroom demonstration purposes by intricately piecing together a platinum coated wire, 9 volt battery, 9 volt battery clip and a glass of water. For more practical uses, such as in cars, engineers have to take many things into consideration, such as the amount of space a tank of hydrogen gas would take up, and how far that tank will last.

https://www.energy.gov/eere/fuelcells/fuel-cells
https://www.researchgate.net/figure/Schematic-illustration-of-a-hydrogen-fuel-cell_fig1_282780148
https://sci-toys.com/scitoys/scitoys/echem/fuel_cell/fuel_cell.html
https://www.popularmechanics.com/cars/hybrid-electric/a22688627/hydrogen-fuel-cell-cars/
Fuel cells is a device that produces electricity using a chemical process. The electricity can be produced by converting energy giving a constant supply of fuel that is fed into the fuel cell. This electricity is made by a reaction that is electrolysis in reverse, using cell potential and electrical current output. It is very similar to how a battery works but the energy isn’t stored in fuel cells. This reaction brings hydrogen and oxygen atoms together providing a constant source of energy. The maximum amount of electrical energy output is when the fuel cell is working in thermodynamically reversible conditions. So the system works when fuel and oxidant streams enter and the product stream exits, although in the process it will loose some energy which will be in the form of heat. For all these equation and formulas it will be based from a hydrogen and oxygen fuel cell. The electrochemical reaction with W being the rate of electrical work and Q is the rate of heat transferred into the system is:
H2(fuel)+O2(oxidant)->W+Q+H2O(product)
The maximum amount of work can be shown by Gibb’s free energy change (n=number of moles, F=Faraday’s constant, and E=reversible potential):
W=dG=-nFE
Although, if the reaction has both the products and reactants in the standard states the equation will be shown as:
dG=-nFEo
So then the maximum cell potential (reversible cell potential) can be found by:
Erev=-(dG)/(nF)
To find the entropy this equation will be used (dG=gibb’s free energy change, dH=total thermal energy, and TdS=heat produced by fuel cell):
dH=dG+TdS
If the entropy found is negative it means the fuel cell is generating heat and if it is positive then the cell is absorbing heat from the environment around the cell. The Nernst equation can be used to see the relationship between the standard potential and the open circuit voltage using the partial pressures at a constant temperature (with hydrogen being the anode and oxygen being the cathode):
H2->2H+2e-
1/2O2+2H+2e- ->H2O
E(T,P)=Eo-(RT/2F)ln[(yH2Ocathode/Psat)/(yH2Panode/Po)*(yO2Pcathode/Po)^1/2]
If standard potential is known the Nernst equation can give an estimate of the voltage at different temperatures and pressures.
https://cset.mnsu.edu/engagethermo/components_fuelcell.html
https://www.intechopen.com/online-first/fuel-cell-thermodynamics
Fuel cells produce electricity through a chemical process – however, a fuel cells differs from a battery due to the constant supply of fuel given to a cell, whereas a battery has a limited amount of electricity to disperse, merely storing rather than creating the energy. They are incredibly reliable, and even used in space programs.
Similarly to a battery, a fuel cell is composed of an anode and cathode, split apart by an electrolyte. The cell performs a reaction that splits electrons off of the continuous flow of fuel at the anode, at which point the electrolyte will allow these oxidized molecules across. This generates an electrical energy by the same means as a battery, but continues to perform this reaction continuously, ordinarily maintaining a voltage of 0.7V, but normally less than 1. Ordinarily, to create the energy necessary for work, many fuel cells can be strung together.
https://cset.mnsu.edu/engagethermo/components_fuelcell.html
There are several different types of fuel cells, that each have a varying electrical efficiency, paired with their own individual operating standards. More information can be pulled from the reference below, however the general electrical efficiency (LHV) ranges from 40% in the case of a Phosphoric Acid fuel cell, or as high as 60% in Alkaline or Solid Oxide fuel cells.
https://www.energy.gov/eere/fuelcells/comparison-fuel-cell-technologies
When considering whether or not fuel cells are environmentally friendly, the key is to look at how the electricity is generated. By itself, fuel cells do not produce a significant number of pollutants or nanoparticles to cause environmental harm. However, if one were to, for example, draw out the electricity from a major power grid, already running on non-renewable energy, to generate the hydrogen required using hydro-electrolysis, the CO2 emissions per kilowatt hour of electricity would be far too high. At present, industrial hydrogen is predominately obtained from natural gas, which, although better than coal or oil, is still unfavorable. If we could instead, however, obtain the hydrogen through solar power, this would be tremendously better.
In any case, the most prominent pollutants caused by fuel cells are NOx, SO2 and CO2. NOx reacts to form smog and acid raid, and also is central to the formation of fine particles (PM). SO2 combines with water and air to form sulfuric acid: the main component of acid rain. CO2 increases the greenhouse effect, trapping thermal energy in the atmosphere and worsening global warming.
As stated previously, reducing these pollutants through solar-generated hydrogen would be the best way to go.
Sources:
http://chfcc.org/resources/fuel-cell-environmental-impact/
https://www.sciencedaily.com/releases/2015/07/150715113313.htm
Everyones views are different especially when it comes to the environment and what is right and what is wrong. We believe that fuel cells are a better option for our environment. It’s a step in the right direction in regards to saving our nonrenewable resources. No, fuel cells aren’t quite perfect yet but they are at least slightly better than coal or other non-renewable energy sources. Fuel cells still do release some pollutants, some more than others, but there could be ways in changing the energy source in the future to limit the pollutants, like solar-generated hydrogen.
Recent Comments